卷积神经网络(CNN)前向传播算法

在卷积神经网络(CNN)模型结构中，我们对CNN的模型结构做了总结，这里我们就在CNN的模型基础上，看看CNN的前向传播算法是什么样子的。重点会和传统的DNN比较讨论。

1. 回顾CNN的结构

　　　　在上一篇里，我们已经讲到了CNN的结构，包括输出层，若干的卷积层+ReLU激活函数，若干的池化层，DNN全连接层，以及最后的用Softmax激活函数的输出层。这里我们用一个彩色的汽车样本的图像识别再从感官上回顾下CNN的结构。图中的CONV即为卷积层，POOL即为池化层，而FC即为DNN全连接层，包括了我们上面最后的用Softmax激活函数的输出层。

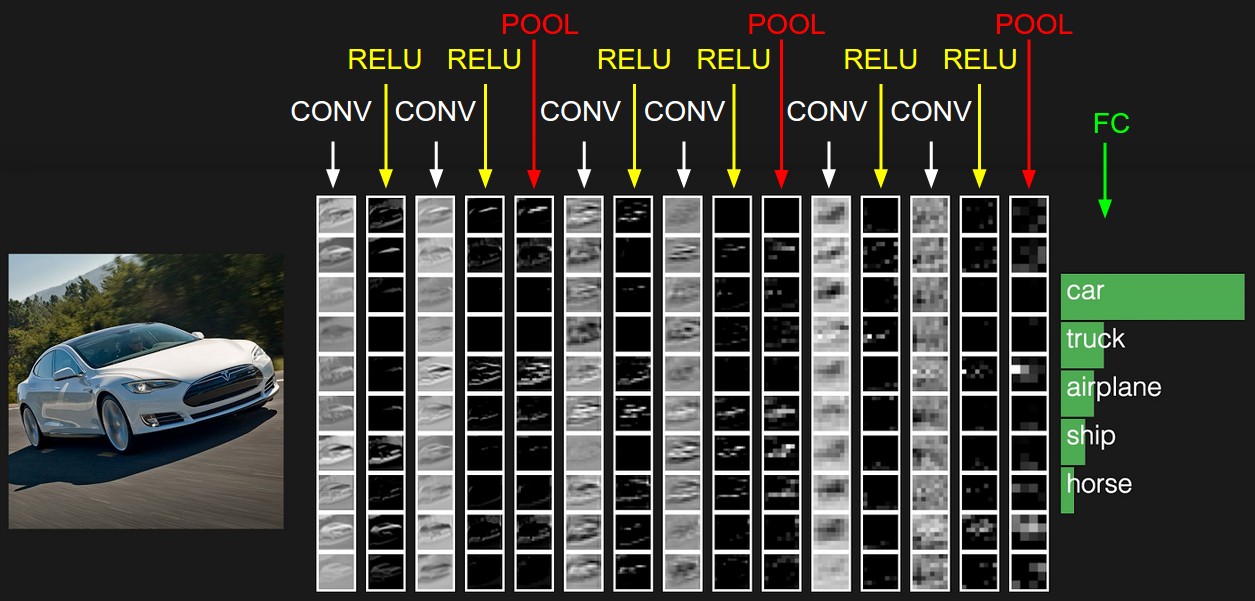
　　　　从上图可以看出，要理顺CNN的前向传播算法，重点是输入层的前向传播，卷积层的前向传播以及池化层的前向传播。而DNN全连接层和用Softmax激活函数的输出层的前向传播算法我们在讲DNN时已经讲到了。

2. CNN输入层前向传播到卷积层

　　　　输入层的前向传播是CNN前向传播算法的第一步。一般输入层对应的都是卷积层，因此我们标题是输入层前向传播到卷积层。

　　　　我们这里还是以图像识别为例。

　　　　先考虑最简单的，样本都是二维的黑白图片。这样输入层X就是一个矩阵，矩阵的值等于图片的各个像素位置的值。这时和卷积层相连的卷积核W就也是矩阵。

　　　　如果样本都是有RGB的彩色图片，这样输入X就是3个矩阵，即分别对应R，G和B的矩阵，或者说是一个张量。这时和卷积层相连的卷积核W就也是张量，对应的最后一维的维度为3.即每个卷积核都是3个子矩阵组成。

　　　　同样的方法，对于3D的彩色图片之类的样本，我们的输入X可以是4维，5维的张量，那么对应的卷积核W也是个高维的张量。

　　　　不管维度多高，对于我们的输入，前向传播的过程可以表示为：$a^2= \sigma(z^2) = \sigma(a^1*W^2 +b^2)$

　　　　其中，上标代表层数，星号代表卷积，而b代表我们的偏倚,$\sigma$为激活函数，这里一般都是ReLU。

　　　　和DNN的前向传播比较一下，其实形式非常的像，只是我们这儿是张量的卷积，而不是矩阵的乘法。同时由于W是张量，那么同样的位置，W参数的个数就比DNN多很多了。

　　　　为了简化我们的描述，本文后面如果没有特殊说明，我们都默认输入是3维的张量，即用RBG可以表示的彩色图片。

　　　　这里需要我们自己定义的CNN模型参数是：

　　　　1） 一般我们的卷积核不止一个，比如有K个，那么我们输入层的输出，或者说第二层卷积层的对应的输入就K个。

　　　　2） 卷积核中每个子矩阵的的大小，一般我们都用子矩阵为方阵的卷积核，比如FxF的子矩阵。

　　　　3） 填充padding（以下简称P），我们卷积的时候，为了可以更好的识别边缘，一般都会在输入矩阵在周围加上若干圈的0再进行卷积，加多少圈则P为多少。

　　　　4） 步幅stride（以下简称S），即在卷积过程中每次移动的像素距离大小。

　　　　这些参数我们在上一篇都有讲述。

3. 隐藏层前向传播到卷积层

　　　　现在我们再来看普通隐藏层前向传播到卷积层时的前向传播算法。

　　　　假设隐藏层的输出是M个矩阵对应的三维张量，则输出到卷积层的卷积核也是M个子矩阵对应的三维张量。这时表达式和输入层的很像，也是$a^l= \sigma(z^l) =\sigma(a^{l-1}*W^l +b^l)$

　　　　其中，上标代表层数，星号代表卷积，而b代表我们的偏倚,$\sigma$为激活函数，这里一般都是ReLU。

　　　　也可以写成M个子矩阵卷积后对应位置相加的形式，即：$a^l= \sigma(z^l) =\sigma(\sum\limits_{k=1}^{M}z_k^l) = \sigma(\sum\limits_{k=1}^{M}(a_k^{l-1}*W_k^l +b_k^l))$

　　　　和上一节唯一的区别仅仅在于，这里的输入是隐藏层来的，而不是我们输入的原始图片样本形成的矩阵。

　　　　需要我们定义的CNN模型参数也和上一节一样，这里我们需要定义卷积核的个数K，卷积核子矩阵的维度F，填充大小P以及步幅S。

4. 隐藏层前向传播到池化层

　　　　池化层的处理逻辑是比较简单的，我们的目的就是对输入的矩阵进行缩小概括。比如输入的若干矩阵是NxN维的，而我们的池化大小是kxk的区域，则输出的矩阵都是$\frac{N}{k} \times \frac{N}{k}$维的。

　　　　这里需要需要我们定义的CNN模型参数是：

　　　　1）池化区域的大小k

　　　　2）池化的标准，一般是MAX或者Average。

5. 隐藏层前向传播到全连接层

　　　　由于全连接层就是普通的DNN模型结构，因此我们可以直接使用DNN的前向传播算法逻辑，即：$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$

　　　　这里的激活函数一般是sigmoid或者tanh。

　　　　经过了若干全连接层之后，最后的一层为Softmax输出层。此时输出层和普通的全连接层唯一的区别是，激活函数是softmax函数。

　　　　这里需要需要我们定义的CNN模型参数是：

　　　　1）全连接层的激活函数

　　　　2）全连接层各层神经元的个数

6. CNN前向传播算法小结

　　　　有了上面的基础，我们现在总结下CNN的前向传播算法。

　　　　输入：1个图片样本，CNN模型的层数L和所有隐藏层的类型，对于卷积层，要定义卷积核的大小K，卷积核子矩阵的维度F，填充大小P，步幅S。对于池化层，要定义池化区域大小k和池化标准（MAX或Average），对于全连接层，要定义全连接层的激活函数（输出层除外）和各层的神经元个数。

　　　　输出：CNN模型的输出$a^L$

　　　　1) 根据输入层的填充大小P，填充原始图片的边缘，得到输入张量$a^1$。

　　　　2）初始化所有隐藏层的参数W,b

　　　　3）for l=2 to L-1:

　　　　　　a) 如果第l层是卷积层,则输出为$a^l= ReLU(z^l) = ReLU(a^{l-1}*W^l +b^l)$

　　　　　 b) 如果第l层是池化层,则输出为$a^l= pool(a^{l-1})$, 这里的pool指按照池化区域大小k和池化标准将输入张量缩小的过程。

　　　　　　c) 如果第l层是全连接层,则输出为$a^l= \sigma(z^l) =\sigma(W^la^{l-1} +b^l)$

　　　　4)对于输出层第L层:$a^L=softmax(z^L)= softmax(W^La^{L-1}+b^L)$