深度神经网络（DNN）模型与前向传播算法

深度神经网络（Deep Neural Networks， 以下简称DNN）是深度学习的基础，而要理解DNN，首先我们要理解DNN模型，下面我们就对DNN的模型与前向传播算法做一个总结。

1. 从感知机到神经网络

在感知机原理小结中，我们介绍过感知机的模型，它是一个有若干输入和一个输出的模型，如下图:

输出和输入之间学习到一个线性关系，得到中间输出结果：$z=\sum\limits_{i=1}^mw_ix_i + b$

接着是一个神经元激活函数:

$sign(z)= \begin{cases} -1& {z<0}\\ 1& {z\geq 0} \end{cases}$

从而得到我们想要的输出结果1或者-1。

这个模型只能用于二元分类，且无法学习比较复杂的非线性模型，因此在工业界无法使用。

而神经网络则在感知机的模型上做了扩展，总结下主要有三点：

1）加入了隐藏层，隐藏层可以有多层，增强模型的表达能力，如下图实例，当然增加了这么多隐藏层模型的复杂度也增加了好多。

2）输出层的神经元也可以不止一个输出，可以有多个输出，这样模型可以灵活的应用于分类回归，以及其他的机器学习领域比如降维和聚类等。多个神经元输出的输出层对应的一个实例如下图，输出层现在有4个神经元了。

3） 对激活函数做扩展，感知机的激活函数是sign(z),虽然简单但是处理能力有限，因此神经网络中一般使用的其他的激活函数，比如我们在逻辑回归里面使用过的Sigmoid函数，即：$f(z)=\frac{1}{1+e^{-z}}$

还有后来出现的tanx, softmax,和ReLU等。通过使用不同的激活函数，神经网络的表达能力进一步增强。对于各种常用的激活函数，我们在后面再专门讲。

2. DNN的基本结构

上一节我们了解了神经网络基于感知机的扩展，而DNN可以理解为有很多隐藏层的神经网络。这个很多其实也没有什么度量标准, 多层神经网络和深度神经网络DNN其实也是指的一个东西，当然，DNN有时也叫做多层感知机（Multi-Layer perceptron,MLP）, 名字实在是多。后面我们讲到的神经网络都默认为DNN。

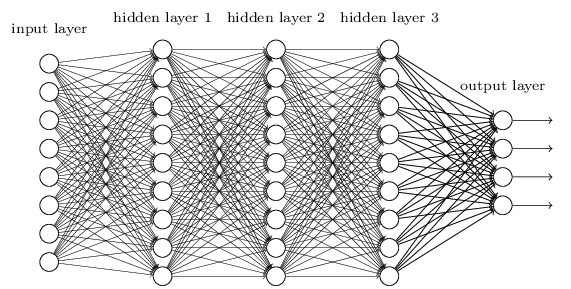
从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层,如下图示例，一般来说第一层是输出层，最后一层是输出层，而中间的层数都是隐藏层。

层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系$z=\sum\limits w_ix_i + b$加上一个激活函数$\sigma(z)$。

由于DNN层数多，则我们的线性关系系数w和偏倚b的数量也就是很多了。具体的参数在DNN是如何定义的呢？

首先我们来看看线性关系系数w的定义。以下图一个三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的线性系数定义为$w_{24}^3$。上标3代表线性系数w所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。你也许会问，为什么不是$w_{42}^3$, 而是$w_{24}^3$呢？这主要是为了便于模型用于矩阵表示运算，如果是$w_{24}^3$而每次进行矩阵运算是$w^Tx+b$，需要进行转置。将输出的索引放在前面的话，则线性运算不用转置,即直接为$wx+b$。总结下，第l-1层的第k个神经元到第l层的第j个神经元的线性系数定义为$w_{jk}^l$。注意，输入层是没有w参数的。

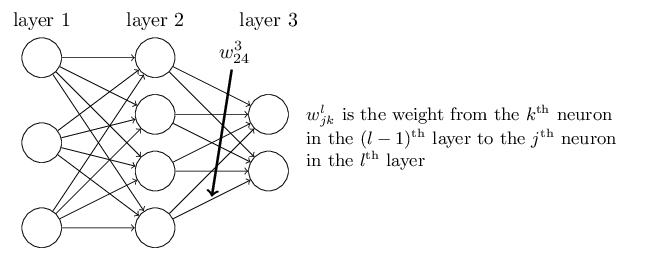
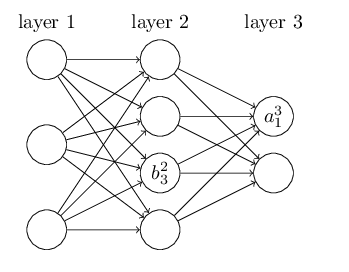
再来看看偏倚b的定义。还是以这个三层的DNN为例，第二层的第三个神经元对应的偏倚定义为$b_3^{2}$。其中，上标2代表所在的层数，下标3代表偏倚所在的神经元的索引。同样的道理，第三个的第一个神经元的偏倚应该表示为$b_1^{3}$。同样的，输入层是没有偏倚参数b的。

3. DNN前向传播算法数学原理

在上一节，我们已经介绍了DNN各层线性关系系数w,偏倚b的定义。假设我们选择的激活函数是$\sigma(z)$，隐藏层和输出层的输出值为a，则对于下图的三层DNN,利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。

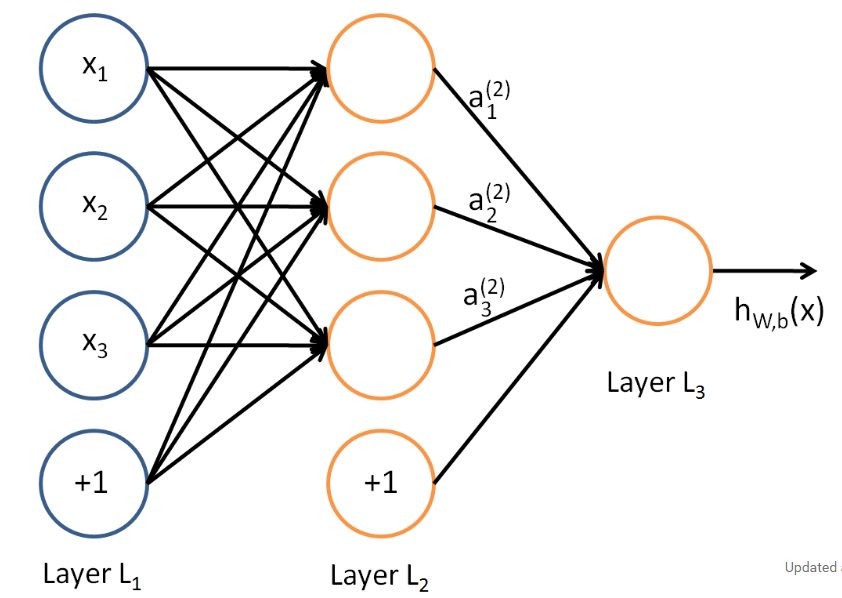
对于第二层的的输出$a_1^2,a_2^2,a_3^2$，我们有：

$a_1^2=\sigma(z_1^2) = \sigma(w_{11}^2x_1 + w_{12}^2x_2 + w_{13}^2x_3 + b_1^{2})$

$a_2^2=\sigma(z_2^2) = \sigma(w_{21}^2x_1 + w_{22}^2x_2 + w_{32}^2x_3 + b_2^{2})$

$a_3^2=\sigma(z_3^2) = \sigma(w_{31}^2x_1 + w_{32}^2x_2 + w_{33}^2x_3 + b_3^{2})$

对于第三层的的输出$a_1^3$，我们有：$a_1^3=\sigma(z_1^3) = \sigma(w_{11}^3a_1^2 + w_{12}^3a_2^2 + w_{13}^3a_3^2 + b_3^{3})$

将上面的例子一般化，假设第l-1层共有m个神经元，则对于第l层的第j个神经元的输出$a_j^l$，我们有：$a_j^l = \sigma(z_j^l) = \sigma(\sum\limits_{k=1}^mw_{jk}^la_k^{l-1} + b_j^l)$

其中，如果l=2,则对于的$a_k^1$即为输入层的$x_k$。

从上面可以看出，使用代数法一个个的表示输出比较复杂，而如果使用矩阵法则比较的简洁。假设第l-1层共有m个神经元，而第l层共有n个神经元，则第l层的线性系数w组成了一个$n \times m$的矩阵$W^l$, 第l层的偏倚b组成了一个$n \times 1$的向量$b^l$ , 第l-1层的的输出a组成了一个$m \times 1$的向量$a^{l-1}$，第l层的的未激活前线性输出z组成了一个$n \times 1$的向量$z^{l}$, 第l层的的输出a组成了一个$n \times 1$的向量$a^{l}$。则用矩阵法表示，第l层的输出为：$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$

这个表示方法简洁漂亮，后面我们的讨论都会基于上面的这个矩阵法表示来。

4. DNN前向传播算法

有了上一节的数学推导，DNN的前向传播算法也就不难了。所谓的DNN的前向传播算法也就是利用我们的若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。

输入: 总层数L，所有隐藏层和输出层对应的矩阵W,偏倚向量b，输入值向量x

输出：输出层的输出$a^L$

1） 初始化$a^1 = x$

2) for l = 2 to L, 计算：$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$

最后的结果即为输出$a^L$。