循环神经网络(RNN)模型与前向反向传播算法

在前面我们讲到了DNN，以及DNN的特例CNN的模型和前向反向传播算法，这些算法都是前向反馈的，模型的输出和模型本身没有关联关系。今天我们就讨论另一类输出和模型间有反馈的神经网络：循环神经网络(Recurrent Neural Networks ，以下简称RNN)，它广泛的用于自然语言处理中的语音识别，手写书别以及机器翻译等领域。

1. RNN概述

　　　　在前面讲到的DNN和CNN中，训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决，就是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。

　　　　而对于这类问题，RNN则比较的擅长。那么RNN是怎么做到的呢？RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引$\tau$的。对于这其中的任意序列索引号t,它对应的输入是对应的样本序列中的$x^{(t)}$。而模型在序列索引号t位置的隐藏状态$h^{(t)}$，则由$x^{(t)}$和在t-1位置的隐藏状态$h^{(t-1)}$共同决定。在任意序列索引号t，我们也有对应的模型预测输出$o^{(t)}$。通过预测输出$o^{(t)}$和训练序列真实输出$y^{(t)}$,以及损失函数$L^{(t)}$，我们就可以用DNN类似的方法来训练模型，接着用来预测测试序列中的一些位置的输出。

　　　　下面我们来看看RNN的模型。

2. RNN模型

　　　　RNN模型有比较多的变种，这里介绍最主流的RNN模型结构如下：

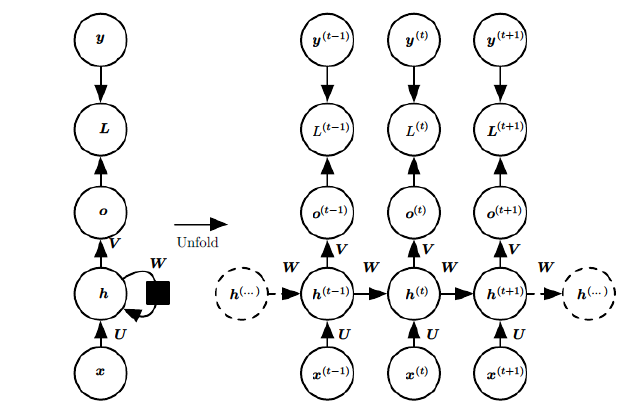
　　　　上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。

　　　　这幅图描述了在序列索引号t附近RNN的模型。其中：

　　　　1）$x^{(t)}$代表在序列索引号t时训练样本的输入。同样的，$x^{(t-1)}$和$x^{(t+1)}$代表在序列索引号t-1和t+1时训练样本的输入。

　　　　2）$h^{(t)}$代表在序列索引号t时模型的隐藏状态。$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$共同决定。

　　　　3）$o^{(t)}$代表在序列索引号t时模型的输出。$o^{(t)}$只由模型当前的隐藏状态$h^{(t)}$决定。

　　　　4）$L^{(t)}$代表在序列索引号t时模型的损失函数。

　　　　5）$y^{(t)}$代表在序列索引号t时训练样本序列的真实输出。

　　　　6）U,W,V这三个矩阵是我们的模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。 也正因为是共享了，它体现了RNN的模型的“循环反馈”的思想。　　

3. RNN前向传播算法

　　　　有了上面的模型，RNN的前向传播算法就很容易得到了。

　　　　对于任意一个序列索引号t，我们隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$得到：$h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b)$

　　　　其中$\sigma$为RNN的激活函数，一般为tanh,b为线性关系的偏倚。

　　　　序列索引号t时模型的输出$o^{(t)}$的表达式比较简单：$o^{(t)} = Vh^{(t)} +c$

　　　　在最终在序列索引号t时我们的预测输出为:$\hat{y}^{(t)} = \sigma(o^{(t)})$

　　　　通常由于RNN是识别类的分类模型，所以上面这个激活函数一般是softmax。

　　　　通过损失函数$L^{(t)}$，比如对数似然损失函数，我们可以量化模型在当前位置的损失，即$\hat{y}^{(t)}$和$y^{(t)}$的差距。

4. RNN反向传播算法推导

　　　　有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数U,W,V,b,c。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的U,W,V,b,c在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。

　　　　为了简化描述，这里的损失函数我们为对数损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。

　　　　对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失L为：$L = \sum\limits_{t=1}^{\tau}L^{(t)}$

　　　　其中V,c,的梯度计算是比较简单的：

$\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}$

$\frac{\partial L}{\partial V} =\sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} -y^{(t)}) (h^{(t)})^T$

　　　　但是W,U,b的梯度计算就比较的复杂了。从RNN的模型可以看出，在反向传播时，在在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置t+1时的梯度损失两部分共同决定。对于W在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引t位置的隐藏状态的梯度为：$\delta^{(t)} = \frac{\partial L}{\partial h^{(t)}}$

　　　　这样我们可以像DNN一样从$\delta^{(t+1)}$递推$\delta^{(t)}$。$\delta^{(t)} =\frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-(h^{(t+1)})^2)$

　　　　对于$\delta^{(\tau)}$，由于它的后面没有其他的序列索引了，因此有：$\delta^{(\tau)} =\frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} = V^T(\hat{y}^{(\tau)} - y^{(\tau)})$

　　　　有了$\delta^{(t)}$,计算W,U,b就容易了，这里给出W,U,b的梯度计算表达式：

$\frac{\partial L}{\partial W} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(h^{(t-1)})^T$

$\frac{\partial L}{\partial b}= \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}$

$\frac{\partial L}{\partial U} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(x^{(t)})^T$

　　　　除了梯度表达式不同，RNN的反向传播算法和DNN区别不大，因此这里就不再重复总结了。

5. RNN小结

　　　　上面总结了通用的RNN模型和前向反向传播算法。当然，有些RNN模型会有些不同，自然前向反向传播的公式会有些不一样，但是原理基本类似。

　　　　RNN虽然理论上可以很漂亮的解决序列数据的训练，但是它也像DNN一样有梯度消失时的问题，当序列很长的时候问题尤其严重。因此，上面的RNN模型一般不能直接用于应用领域。在语音识别，手写书别以及机器翻译等NLP领域实际应用比较广泛的是基于RNN模型的一个特例LSTM，下一篇我们就来讨论LSTM模型。