Gibbs采样

M-H采样有两个缺点：一是需要计算接受率，在高维时计算量大。并且由于接受率的原因导致算法收敛时间变长。二是有些高维数据，特征的条件概率分布好求，但是特征的联合分布不好求。因此需要一个好的方法来改进M-H采样，这就是我们下面讲到的Gibbs采样。

1. 重新寻找合适的细致平稳条件

如果非周期马尔科夫链的状态转移矩阵P和概率分布$\pi(x)$对于所有的i,j满足：$\pi(i)P(i,j) = \pi(j)P(j,i)$

则称概率分布$\pi(x)$是状态转移矩阵P的平稳分布。

在M-H采样中我们通过引入接受率使细致平稳条件满足。现在我们换一个思路。

从二维的数据分布开始，假设$\pi(x_1,x_2)$是一个二维联合数据分布，观察第一个特征维度相同的两个点$A(x_1^{(1)},x_2^{(1)})$和$B(x_1^{(1)},x_2^{(2)})$，容易发现下面两式成立：$\pi(x_1^{(1)},x_2^{(1)}) \pi(x_2^{(2)} | x_1^{(1)}) = \pi(x_1^{(1)})\pi(x_2^{(1)}|x_1^{(1)}) \pi(x_2^{(2)} | x_1^{(1)})\pi(x_1^{(1)},x_2^{(2)}) \pi(x_2^{(1)} | x_1^{(1)}) = \pi(x_1^{(1)}) \pi(x_2^{(2)} | x_1^{(1)})\pi(x_2^{(1)}|x_1^{(1)})$

由于两式的右边相等，因此我们有：$\pi(x_1^{(1)},x_2^{(1)}) \pi(x_2^{(2)} | x_1^{(1)}) = \pi(x_1^{(1)},x_2^{(2)}) \pi(x_2^{(1)} | x_1^{(1)})$

也就是：$\pi(A) \pi(x_2^{(2)} | x_1^{(1)}) = \pi(B) \pi(x_2^{(1)} | x_1^{(1)})$

观察上式再观察细致平稳条件的公式，我们发现在$x_1 = x_1^{(1)}$这条直线上，如果用条件概率分布$\pi(x_2| x_1^{(1)})$作为马尔科夫链的状态转移概率，则任意两个点之间的转移满足细致平稳条件！这真是一个开心的发现，同样的道理，在在$x_2 = x_2^{(1)}$这条直线上，如果用条件概率分布$\pi(x_1| x_2^{(1)})$作为马尔科夫链的状态转移概率，则任意两个点之间的转移也满足细致平稳条件。那是因为假如有一点$C(x_1^{(2)},x_2^{(1)})$,我们可以得到：$\pi(A) \pi(x_1^{(2)} | x_2^{(1)}) = \pi(C) \pi(x_1^{(1)} | x_2^{(1)})$

基于上面的发现，我们可以这样构造分布$\pi(x_1,x_2)$的马尔可夫链对应的状态转移矩阵

$P(A \to B) = \pi(x_2^{(B)}|x_1^{(1)})\;\; if\; x_1^{(A)} = x_1^{(B)} =x_1^{(1)}$

$P(A \to C) = \pi(x_1^{(C)}|x_2^{(1)})\;\; if\; x_2^{(A)} = x_2^{(C)} =x_2^{(1)}$

$P(A \to D) = 0\;\; else$

有了上面这个状态转移矩阵，我们很容易验证平面上的任意两点E,F，满足细致平稳条件：$\pi(E)P(E \to F) = \pi(F)P(F \to E)$

2. 二维Gibbs采样

利用上一节找到的状态转移矩阵，我们就得到了二维Gibbs采样，这个采样需要两个维度之间的条件概率。具体过程如下：

1）输入平稳分布$\pi(x_1,x_2)$，设定状态转移次数阈值$n_1$，需要的样本个数$n_2$

2）随机初始化初始状态值$x_1^{(1)}$和$x_2^{(1)}$

3）for t = 0 to $n_1 +n_2-1$:

a) 从条件概率分布$P(x_2|x_1^{(t)})$中采样得到样本$x_2^{t+1}$

b) 从条件概率分布$P(x_1|x_2^{(t+1)})$中采样得到样本$x_1^{t+1}$

样本集$\{(x_1^{(n_1)}, x_2^{(n_1)}), (x_1^{(n_1+1)}, x_2^{(n_1+1)}), ..., (x_1^{(n_1+n_2-1)}, x_2^{(n_1+n_2-1)})\}$即为我们需要的平稳分布对应的样本集。

整个采样过程中，我们通过轮换坐标轴，采样的过程为：$(x_1^{(1)}, x_2^{(1)}) \to (x_1^{(1)}, x_2^{(2)}) \to (x_1^{(2)}, x_2^{(2)}) \to ... \to (x_1^{(n_1+n_2-1)}, x_2^{(n_1+n_2-1)})$

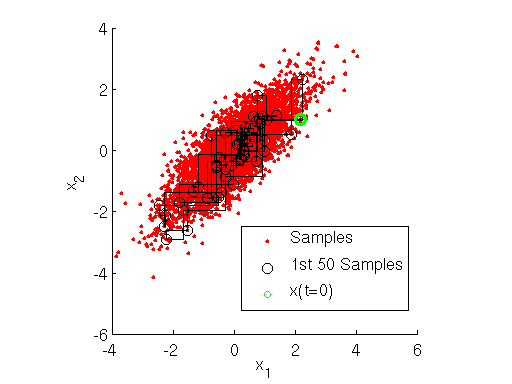
用下图可以很直观的看出，采样是在两个坐标轴上不停的轮换的。当然，坐标轴轮换不是必须的，我们也可以每次随机选择一个坐标轴进行采样。不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

3. 多维Gibbs采样

上面的这个算法推广到多维的时候也是成立的。比如一个n维的概率分布$\pi(x_1,x_2,...x_n)$，我们可以通过在n个坐标轴上轮换采样，来得到新的样本。对于轮换到的任意一个坐标轴$x_i$上的转移，马尔科夫链的状态转移概率为$P(x_i|x_1,x_2,...,x_{i-1},x_{i+1},...,x_n)$，即固定n-1个坐标轴，在某一个坐标轴上移动。

具体的算法过程如下：

1）输入平稳分布$\pi(x_1,x_2,...,x_n)$或者对应的所有特征的条件概率分布，设定状态转移次数阈值$n_1$，需要的样本个数$n_2$

2）随机初始化初始状态值$(x_1^{(1)},x_2^{(1)},...,x_n^{(1)}$

3）for t = 0 to $n_1 +n_2-1$:

a) 从条件概率分布$P(x_1|x_2^{(t)}, x_3^{(t)},...,x_n^{(t)})$中采样得到样本$x_1^{t+1}$

b) 从条件概率分布$P(x_2|x_1^{(t+1)}, x_3^{(t)}, x_4^{(t)},...,x_n^{(t)})$中采样得到样本$x_2^{t+1}$

c)...

d) 从条件概率分布$P(x_j|x_1^{(t+1)}, x_2^{(t+1)},..., x_{j-1}^{(t+1)},x_{j+1}^{(t)}...,x_n^{(t)})$中采样得到样本$x_j^{t+1}$

e)...

f) 从条件概率分布$P(x_n|x_1^{(t+1)}, x_2^{(t+1)},...,x_{n-1}^{(t+1)})$中采样得到样本$x_n^{t+1}$

样本集${(x_1^{(n_1)}, x_2^{(n_1)},..., x_n^{(n_1)}), ..., (x_1^{(n_1+n_2-1)}, x_2^{(n_1+n_2-1)},...,x_n^{(n_1+n_2-1)})}$即为我们需要的平稳分布对应的样本集。

整个采样过程和Lasso回归的坐标轴下降法算法非常类似，只不过Lasso回归是固定n-1个特征，对某一个特征求极值。而Gibbs采样是固定n-1个特征在某一个特征采样。

同样的，轮换坐标轴不是必须的，我们可以随机选择某一个坐标轴进行状态转移，只不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

4. 二维Gibbs采样实例

这里给出一个Gibbs采样的例子。假设我们要采样的是一个二维正态分布$Norm(\mu,\Sigma)$,其中：

$\mu = (\mu_1,\mu_2) = (5,-1)$

$\Sigma = \left( \begin{array}{ccc} \sigma_1^2&\rho\sigma_1\sigma_2 \ \rho\sigma_1\sigma_2 &\sigma_2^2 \end{array} \right) = \left( \begin{array}{ccc} 1&1 \ 1&4 \end{array} \right)$

而采样过程中的需要的状态转移条件分布为：$P(x_1|x_2) = Norm\left ( \mu _1+\rho \sigma_1/\sigma_2 \left ( x _2-\mu _2 \right ), (1-\rho ^2)\sigma_1^2 \right )P(x_2|x_1) = Norm\left ( \mu _2+\rho \sigma_2/\sigma_1 \left ( x _1-\mu _1 \right ), (1-\rho ^2)\sigma_2^2 \right )$

具体的代码如下：

import random
import math
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal

samplesource = multivariate_normal(mean=[5,-1], cov=[[1,1],[1,4]])

def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * math.sqrt(s2 / s1) * (x - m1), math.sqrt(1 - rho ** 2) * s2))

def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * math.sqrt(s1 / s2) * (y - m2), math.sqrt(1 - rho ** 2) * s1))

N = 5000
K = 20
x_res = []
y_res = []
z_res = []
m1 = 5
m2 = -1
s1 = 1
s2 = 4

rho = 0.5
y = m2

for i in xrange(N):
    for j in xrange(K):
        x = p_xgiveny(y, m1, m2, s1, s2)
        y = p_ygivenx(x, m1, m2, s1, s2)
        z = samplesource.pdf([x,y])
        x_res.append(x)
        y_res.append(y)
        z_res.append(z)

num_bins = 50
plt.hist(x_res, num_bins, normed=1, facecolor='green', alpha=0.5)
plt.hist(y_res, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.title('Gibbs Sampler')
plt.show()

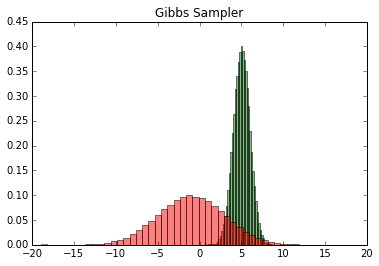
输出的两个特征各自的分布如下：

然后我们看看样本集生成的二维正态分布，代码如下：

fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(x_res, y_res, z_res,marker='o')
plt.show()

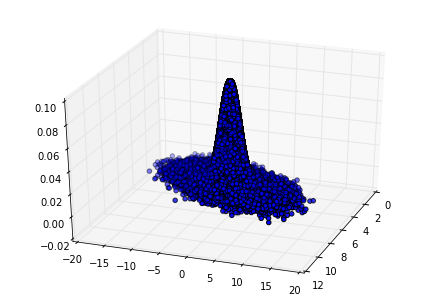
输出的正态分布图如下：

5. Gibbs采样小结

由于Gibbs采样在高维特征时的优势，目前我们通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的,这时M-H采样仍然成立。

有了Gibbs采样来获取概率分布的样本集，有了蒙特卡罗方法来用样本集模拟求和，他们一起就奠定了MCMC算法在大数据时代高维数据模拟求和时的作用。