GAN原理
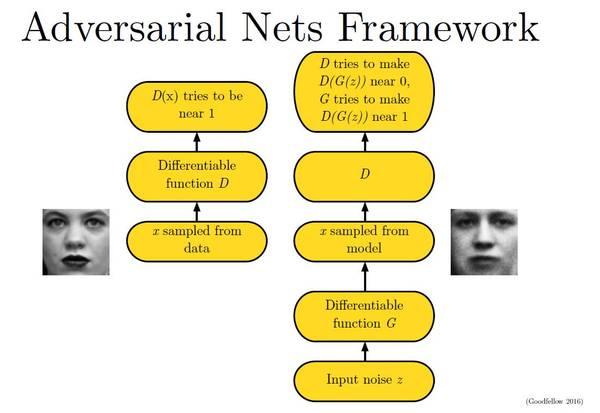
Generative Adversarial Network,就是大家耳熟能详的GAN,由Ian Goodfellow首先提出,在这两年更是深度学习中最热门的东西,仿佛什么东西都能由GAN做出来。我最近刚入门GAN,看了些资料,做一些笔记。
1.Generation
什么是生成(generation)?就是模型通过学习一些数据,然后生成类似的数据。让机器看一些动物图片,然后自己来产生动物的图片,这就是生成。
以前就有很多可以用来生成的技术了,比如auto-encoder(自编码器),结构如下图:
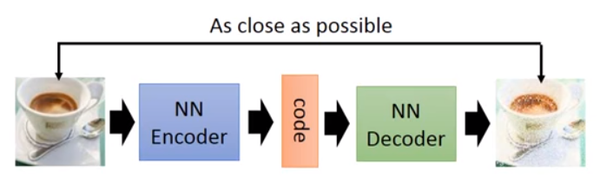
你训练一个encoder,把input转换成code,然后训练一个decoder,把code转换成一个image,然后计算得到的image和input之间的MSE(mean square error),训练完这个model之后,取出后半部分NN Decoder,输入一个随机的code,就能generate一个image。
但是auto-encoder生成image的效果,当然看着很别扭啦,一眼就能看出真假。所以后来还提出了比如VAE这样的生成模型,我对此也不是很了解,在这就不细说。
上述的这些生成模型,其实有一个非常严重的弊端。比如VAE,它生成的image是希望和input越相似越好,但是model是如何来衡量这个相似呢?model会计算一个loss,采用的大多是MSE,即每一个像素上的均方差。loss小真的表示相似嘛?
比如这两张图,第一张,我们认为是好的生成图片,第二张是差的生成图片,但是对于上述的model来说,这两张图片计算出来的loss是一样大的,所以会认为是一样好的图片。
这就是上述生成模型的弊端,用来衡量生成图片好坏的标准并不能很好的完成想要实现的目的。于是就有了下面要讲的GAN。
2.GAN
大名鼎鼎的GAN是如何生成图片的呢?首先大家都知道GAN有两个网络,一个是generator,一个是discriminator,从二人零和博弈中受启发,通过两个网络互相对抗来达到最好的生成效果。流程如下:
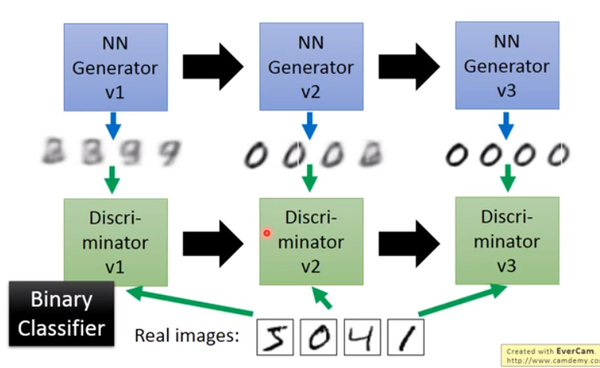
主要流程类似上面这个图。首先,有一个一代的generator,它能生成一些很差的图片,然后有一个一代的discriminator,它能准确的把生成的图片,和真实的图片分类,简而言之,这个discriminator就是一个二分类器,对生成的图片输出0,对真实的图片输出1。
接着,开始训练出二代的generator,它能生成稍好一点的图片,能够让一代的discriminator认为这些生成的图片是真实的图片。然后会训练出一个二代的discriminator,它能准确的识别出真实的图片,和二代generator生成的图片。以此类推,会有三代,四代。。。n代的generator和discriminator,最后discriminator无法分辨生成的图片和真实图片,这个网络就拟合了。
这就是GAN,运行过程就是这么的简单。这就结束了嘛?显然没有,下面还要介绍一下GAN的原理。
3.原理
首先我们知道真实图片集的分布,x是一个真实图片,可以想象成一个向量,这个向量集合的分布就是
。我们需要生成一些也在这个分布内的图片,如果直接就是这个分布的话,怕是做不到的。
我们现在有的generator生成的分布可以假设为,这是一个由
控制的分布,
是这个分布的参数(如果是高斯混合模型,那么
就是每个高斯分布的平均值和方差)
假设我们在真实分布中取出一些数据,,我们想要计算一个似然
对于这些数据,在生成模型中的似然就是
我们想要最大化这个似然,等价于让generator生成那些真实图片的概率最大。这就变成了一个最大似然估计的问题了,我们需要找到一个来最大化这个似然。
寻找一个来最大化这个似然,等价于最大化log似然。因为此时这m个数据,是从真实分布中取的,所以也就约等于,真实分布中的所有x在
分布中的log似然的期望。
真实分布中的所有x的期望,等价于求概率积分,所以可以转化成积分运算,因为减号后面的项和无关,所以添上之后还是等价的。然后提出共有的项,括号内的反转,max变min,就可以转化为KL divergence的形式了,KL divergence描述的是两个概率分布之间的差异。
所以最大化似然,让generator最大概率的生成真实图片,也就是要找一个让
更接近于
那如何来找这个最合理的呢?我们可以假设
是一个神经网络。
首先随机一个向量z,通过G(z)=x这个网络,生成图片x,那么我们如何比较两个分布是否相似呢?只要我们取一组sample z,这组z符合一个分布,那么通过网络就可以生成另一个分布,然后来比较与真实分布
大家都知道,神经网络只要有非线性激活函数,就可以去拟合任意的函数,那么分布也是一样,所以可以用一直正态分布,或者高斯分布,取样去训练一个神经网络,学习到一个很复杂的分布。
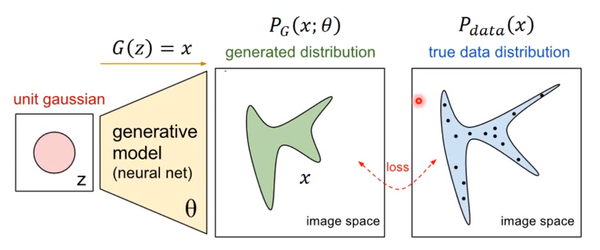
如何来找到更接近的分布,这就是GAN的贡献了。先给出GAN的公式:
这个式子的好处在于,固定G,就表示
和
之间的差异,然后要找一个最好的G,让这个最大值最小,也就是两个分布之间的差异最小。
表面上看这个的意思是,D要让这个式子尽可能的大,也就是对于x是真实分布中,D(x)要接近与1,对于x来自于生成的分布,D(x)要接近于0,然后G要让式子尽可能的小,让来自于生成分布中的x,D(x)尽可能的接近1
现在我们先固定G,来求解最优的D

 对于一个给定的x,得到最优的D如上图,范围在(0,1)内,把最优的D带入
对于一个给定的x,得到最优的D如上图,范围在(0,1)内,把最优的D带入,可以得到:

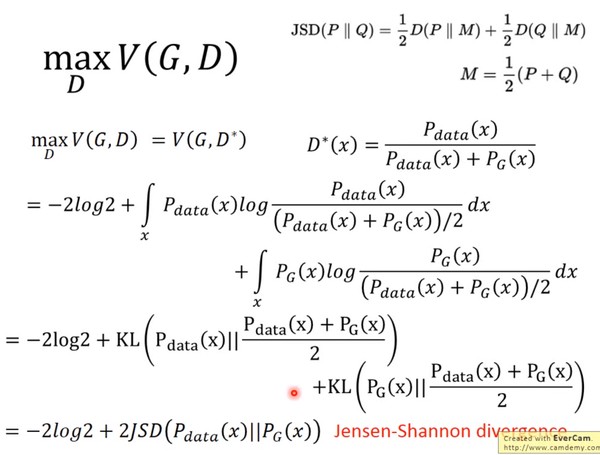 JS divergence是KL divergence的对称平滑版本,表示了两个分布之间的差异,这个推导就表明了上面所说的,固定G,
JS divergence是KL divergence的对称平滑版本,表示了两个分布之间的差异,这个推导就表明了上面所说的,固定G,表示两个分布之间的差异,最小值是-2log2,最大值为0。
现在我们需要找个G,来最小化,观察上式,当
时,G是最优的。
4.训练
有了上面推导的基础之后,我们就可以开始训练GAN了。结合我们开头说的,两个网络交替训练,我们可以在起初有一个和
,先训练
找到
,然后固定
开始训练
,训练的过程都可以使用gradient descent,以此类推,训练
但是这里有个问题就是,你可能在的位置取到了
,然后更新
为
,可能
了,但是并不保证会出现一个新的点
使得
,这样更新G就没达到它原来应该要的效果,如下图所示:
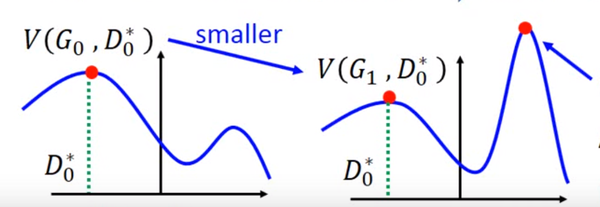
避免上述情况的方法就是更新G的时候,不要更新G太多。
知道了网络的训练顺序,我们还需要设定两个loss function,一个是D的loss,一个是G的loss。下面是整个GAN的训练具体步骤:

上述步骤在机器学习和深度学习中也是非常常见,易于理解。
5.存在的问题
但是上面G的loss function还是有一点小问题,下图是两个函数的图像:
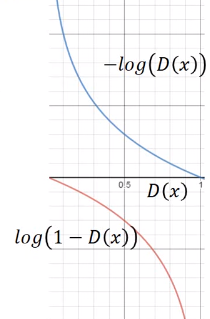
是我们计算时G的loss function,但是我们发现,在D(x)接近于0的时候,这个函数十分平滑,梯度非常的小。这就会导致,在训练的初期,G想要骗过D,变化十分的缓慢,而上面的函数,趋势和下面的是一样的,都是递减的。但是它的优势是在D(x)接近0的时候,梯度很大,有利于训练,在D(x)越来越大之后,梯度减小,这也很符合实际,在初期应该训练速度更快,到后期速度减慢。
所以我们把G的loss function修改为,这样可以提高训练的速度。
还有一个问题,在其他paper中提出,就是经过实验发现,经过许多次训练,loss一直都是平的,也就是,JS divergence一直都是log2,
和
完全没有交集,但是实际上两个分布是有交集的,造成这个的原因是因为,我们无法真正计算期望和积分,只能使用sample的方法,如果训练的过拟合了,D还是能够完全把两部分的点分开,如下图:

对于这个问题,我们是否应该让D变得弱一点,减弱它的分类能力,但是从理论上讲,为了让它能够有效的区分真假图片,我们又希望它能够powerful,所以这里就产生了矛盾。
还有可能的原因是,虽然两个分布都是高维的,但是两个分布都十分的窄,可能交集相当小,这样也会导致JS divergence算出来=log2,约等于没有交集。
解决的一些方法,有添加噪声,让两个分布变得更宽,可能可以增大它们的交集,这样JS divergence就可以计算,但是随着时间变化,噪声需要逐渐变小。
还有一个问题叫Mode Collapse,如下图:
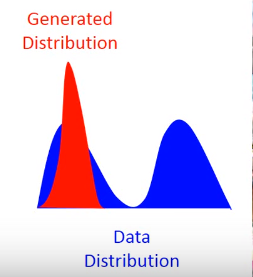
这个图的意思是,data的分布是一个双峰的,但是学习到的生成分布却只有单峰,我们可以看到模型学到的数据,但是却不知道它没有学到的分布。
造成这个情况的原因是,KL divergence里的两个分布写反了
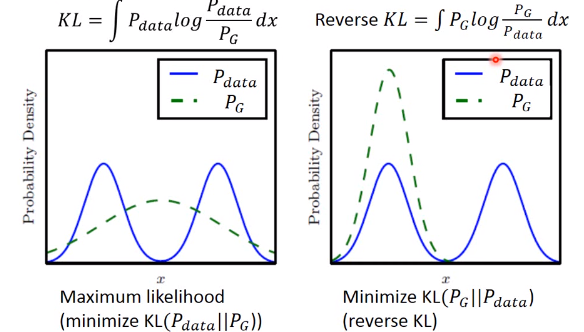
这个图很清楚的显示了,如果是第一个KL divergence的写法,为了防止出现无穷大,所以有出现的地方都必须要有
覆盖,就不会出现Mode Collapse