文本挖掘的分词原理

在做文本挖掘的时候，首先要做的预处理就是分词。英文单词天然有空格隔开容易按照空格分词，但是也有时候需要把多个单词做为一个分词，比如一些名词如“New York”，需要做为一个词看待。而中文由于没有空格，分词就是一个需要专门去解决的问题了。无论是英文还是中文，分词的原理都是类似的，本文就对文本挖掘时的分词原理做一个总结。

1. 分词的基本原理

现代分词都是基于统计的分词，而统计的样本内容来自于一些标准的语料库。假如有一个句子：“小明来到荔湾区”，我们期望语料库统计后分词的结果是："小明/来到/荔湾/区"，而不是“小明/来到/荔/湾区”。那么如何做到这一点呢？

从统计的角度，我们期望"小明/来到/荔湾/区"这个分词后句子出现的概率要比“小明/来到/荔/湾区”大。如果用数学的语言来说说，如果有一个句子S,它有m种分词选项如下：$A_{11}A_{12}...A_{1n_1}A_{21}A_{22}...A_{2n_2}...... ......A_{m1}A_{m2}...A_{mn_m}$

其中下标$n_i$代表第i种分词的词个数。如果我们从中选择了最优的第r种分词方法，那么这种分词方法对应的统计分布概率应该最大，即：$r = arg\;max(i)\;\;P(A_{i1},A_{i2},...,A_{in_i})$

但是我们的概率分布$P(A_{i1},A_{i2},...,A_{in_i})$并不好求出来，因为它涉及到$n_i$个分词的联合分布。在NLP中，为了简化计算，我们通常使用马尔科夫假设，即每一个分词出现的概率仅仅和前一个分词有关，即：$P(A_{ij}|A_{i1},A_{i2},...,A_{i(j-1)}) = P(A_{ij}|A_{i(j-1)})$

在前面我们讲MCMC采样时，也用到了相同的假设来简化模型复杂度。使用了马尔科夫假设，则我们的联合分布就好求了，即：$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i2})...P(A_{in_i}|A_{i(n_i-1)})$

而通过我们的标准语料库，我们可以近似的计算出所有的分词之间的二元条件概率，比如任意两个词$w_1,w_2$，它们的条件概率分布可以近似的表示为：

$P(w_2|w_1) = \frac{P(w_1,w_2)}{P(w_1)} \approx \frac{freq(w_1,w_2)}{freq(w_1)}$

$P(w_1|w_2) = \frac{P(w_2,w_1)}{P(w_2)} \approx \frac{freq(w_1,w_2)}{freq(w_2)}$

其中$freq(w_1,w_2)$表示$w_1,w_2$在语料库中相邻一起出现的次数，而其中$freq(w_1),freq(w_2)$分别表示$w_1,w_2$在语料库中出现的统计次数。

利用语料库建立的统计概率，对于一个新的句子，我们就可以通过计算各种分词方法对应的联合分布概率，找到最大概率对应的分词方法，即为最优分词。

2. N元模型

当然，你会说，只依赖于前一个词太武断了，我们能不能依赖于前两个词呢？即：$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i1},A_{i2})...P(A_{in_i}|A_{i(n_i-2)},A_{i(n_i-1)})$

这样也是可以的，只不过这样联合分布的计算量就大大增加了。我们一般称只依赖于前一个词的模型为二元模型(Bi-Gram model)，而依赖于前两个词的模型为三元模型。以此类推，我们可以建立四元模型，五元模型,...一直到通用的N元模型。越往后，概率分布的计算复杂度越高。当然算法的原理是类似的。

在实际应用中，N一般都较小，一般都小于4，主要原因是N元模型概率分布的空间复杂度为$O(|V|^N)$，其中|V|为语料库大小，而N为模型的元数，当N增大时，复杂度呈指数级的增长。

N元模型的分词方法虽然很好，但是要在实际中应用也有很多问题，首先，某些生僻词，或者相邻分词联合分布在语料库中没有，概率为0。这种情况我们一般会使用拉普拉斯平滑，即给它一个较小的概率值，这个方法在朴素贝叶斯算法原理小结也有讲到。第二个问题是如果句子长，分词有很多情况，计算量也非常大，这时我们可以用下一节维特比算法来优化算法时间复杂度。

3. 维特比算法与分词

为了简化原理描述，我们本节的讨论都是以二元模型为基础。

对于一个有很多分词可能的长句子，我们当然可以用暴力方法去计算出所有的分词可能的概率，再找出最优分词方法。但是用维特比算法可以大大简化求出最优分词的时间。

大家一般知道维特比算法是用于隐式马尔科夫模型HMM解码算法的，但是它是一个通用的求序列最短路径的方法，不光可以用于HMM，也可以用于其他的序列最短路径算法，比如最优分词。

维特比算法采用的是动态规划来解决这个最优分词问题的，动态规划要求局部路径也是最优路径的一部分，很显然我们的问题是成立的。首先我们看一个简单的分词例子："人生如梦境"。它的可能分词可以用下面的概率图表示：

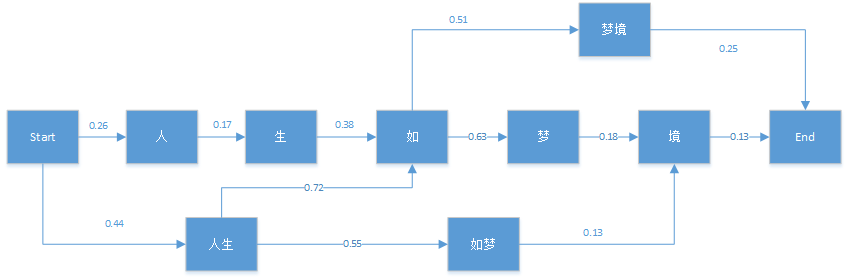
图中的箭头为通过统计语料库而得到的对应的各分词条件概率。比如P(生|人)=0.17。有了这个图，维特比算法需要找到从Start到End之间的一条最短路径。对于在End之前的任意一个当前局部节点，我们需要得到到达该节点的最大概率$\delta$，和记录到达当前节点满足最大概率的前一节点位置$\Psi$。

我们先用这个例子来观察维特比算法的过程。首先我们初始化有：$\delta$(人) = 0.26$\;\;\Psi$(人)$=Start$$\;\;\delta$(人生)$= 0.44\;\;$$\Psi$(人生)=Start

对于节点"生"，它只有一个前向节点，因此有：$\delta$(生) $= \delta$(人)$P$(生|人)$= 0.0442 \;\; \Psi$(生)$=$人

对于节点"如"，就稍微复杂一点了，因为它有多个前向节点，我们要计算出到“如”概率最大的路径：$\delta$(如)$= max \delta$(生)$P$(如|生),$\delta$(人生)P(如|人生)$= max{0.01680, 0.3168} = 0.3168 \;\; \Psi$(如)= 人生

类似的方法可以用于其他节点如下：

$\delta$(如梦) $= \delta$(人生)$P$(如梦|人生)$= 0.242 \;\; \Psi$(如梦)=人生

$\delta$(梦) $= \delta$(如)$P$(梦|如)$= 0.1996 \;\; \Psi$(梦)=如

$\delta$(境)$= max\delta$(梦)$P$(境|梦)$,\delta$(如梦)$P$(境|如梦)}$= max0.0359, 0.0315 = 0.0359 \;\; \Psi$(境)=梦

$\delta$(梦境)$= \delta$(梦境)$P$(梦境|如)$= 0.1585 \;\; \Psi$(梦境)=如

最后我们看看最终节点End:

$\delta(End) = max\delta$(梦境)$P$(End|梦境), $\delta$(境)$P$(End|境)}$= max0.0396, 0.0047\} = 0.0396\;\;\Psi$(End)=梦境

由于最后的最优解为“梦境”，现在我们开始用$\Psi$反推:

$\Psi(End)=$梦境 $\to \Psi$(梦境)=如 $\to \Psi$(如)=人生 $\to \Psi$(人生)=start

从而最终的分词结果为"人生/如/梦境"。是不是很简单呢。

由于维特比算法我会在后面讲隐式马尔科夫模型HMM解码算法时详细解释，这里就不归纳了。

4. 常用分词工具

对于文本挖掘中需要的分词功能，一般我们会用现有的工具。简单的英文分词不需要任何工具，通过空格和标点符号就可以分词了，而进一步的英文分词推荐使用nltk。对于中文分词，则推荐用结巴分词（jieba）。这些工具使用都很简单。你的分词没有特别的需求直接使用这些分词工具就可以了。

5. 结语

分词是文本挖掘的预处理的重要的一步，分词完成后，我们可以继续做一些其他的特征工程，比如向量化（vectorize），TF-IDF以及Hash trick，这些我们后面再讲。