SimRank协同过滤推荐算法

用图模型做协同过滤的方法，包括SimRank系列算法和马尔科夫链系列算法。现在我们就对SimRank算法在推荐系统的应用做一个总结。

1. SimRank推荐算法的图论基础

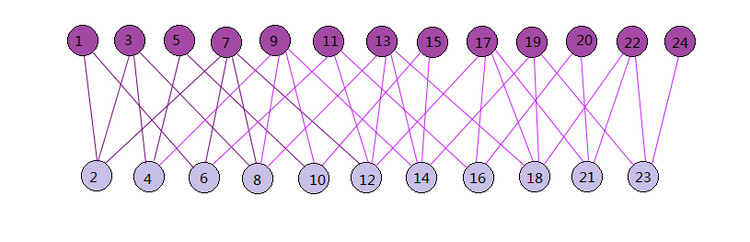
SimRank是基于图论的，如果用于推荐算法，则它假设用户和物品在空间中形成了一张图。而这张图是一个二部图。所谓二部图就是图中的节点可以分成两个子集，而图中任意一条边的两个端点分别来源于这两个子集。一个二部图的例子如下图。从图中也可以看出，二部图的子集内部没有边连接。对于我们的推荐算法中的SimRank，则二部图中的两个子集可以是用户子集和物品子集。而用户和物品之间的一些评分数据则构成了我们的二部图的边。

2. SimRank推荐算法思想

对于用户和物品构成的二部图，如何进行推荐呢？SimRank算法的思想是，如果两个用户相似，则与这两个用户相关联的物品也类似；如果两个物品类似，则与这两个物品相关联的用户也类似。如果回到上面的二部图，假设上面的节点代表用户子集，而下面节点代表物品子集。如果用户1和3类似，那么我们可以说和它们分别相连的物品2和4也类似。

如果我们的二部图是G(V,E)，其中V是节点集合，E是边集合。则某一个子集内两个点的相似度s(a,b)可以用和相关联的另一个子集节点之间相似度表示。即：$s(a,b) = \frac{C}{|I(a)||I(b)|}\sum\limits_{i=1}^{|I_(a)|}\sum\limits_{j=1}^{|I_(b)|}s(I_i(a),I_i(b))$

其中C是一个常数，而$I(a),I(b)$分别代表和a，b相连的二部图另一个子集的节点集合。$s(I_i(a),I_i(b))$即为相连的二部图另一个子集节点之间的相似度。

一种特殊情况是，自己和自己的相似度，我们定义为1。即$s(a,a) =1$。还有一种特殊情况是$I(a),I(b)$有一个为空，即a，b中某一个点没有相连的另一个子集中的点，此时$s(a,b) =0$，将这几种情况综合下，则二部图一个子集内两个点的相似度$s(a,b)$可以表示为：

$s(a,b)= \begin{cases} 1 & {a = b}\\ \frac{C}{|I(a)||I(b)|}\sum\limits_{i=1}^{|I_(a)|}\sum\limits_{j=1}^{|I_(b)|}s(I_i(a),I_i(b)) & {a \neq b, I(a) \neq \emptyset, I(a) \neq \emptyset}\\ 0 & {otherwise} \end{cases}$

如果我们想用上式直接计算两个物品或者两个用户之间的相似度是比较困难的，一般需要通过迭代方式计算。对于$a \neq b, I(a) \neq \emptyset, I(a) \neq \emptyset$时，我们注意到:$s(a,b) = \frac{C}{|I(a)||I(b)|}\sum\limits_{i=1}^{|I_(a)|}\sum\limits_{j=1}^{|I_(b)|}s(I_i(a),I_i(b)) = \frac{C}{|I(a)||I(b)|}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}p_{ia}s(a,b)p_{jb}$

其中p为二部图关联边的权重，而N为二部图节点数。

上面的式子可以继续转化为：$s(a,b) = C\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\Bigg(\frac{p_{ia}}{\sum\limits_{i=1}^{N}p_{ia}}\Bigg)s(a,b)\Bigg(\frac{p_{jb}}{\sum\limits_{j=1}^{N}p_{jb}}\Bigg)$

如果用矩阵表示，则相似度矩阵$S = CW^TSW$, 其中W是将权重值p构成的矩阵P归一化后的矩阵。

但是由于节点和自己的相似度为1，即我们的矩阵S的对角线上的值都应该改为1，那么我们可以去掉对角线上的值，再加上单位矩阵，得到对角线为1的相似度矩阵。即：$S = CW^TSW + I - Diag(diag(CW^TSW))$

其中$diag(CW^TSW)$是矩阵$CW^TSW$的对角线元素构成的向量，而$Diag(diag(CW^TSW))$将这个向量构成对角矩阵。

只要我们对S矩阵按照上式进行若干轮迭代，当S矩阵的值基本稳定后我们就得到了二部图的相似度矩阵，进而可以利用用户与用户的相似度度量，物品与物品的相似度度量进行有针对性的推荐。

3. SimRank算法流程

现在我们对SimRank算法流程做一个总结。

输入：二部图对应的转移矩阵W，阻尼常数C，最大迭代次数k

输出：子集相似度矩阵S：

1) 将相似度S的初始值设置为单位矩阵I.

2) 对于i=1,2...k:

a)$temp = CW^TSW$

b)$S = temp + I - Diag(diag(temp))$

以上基于普通的SimRank算法流程。当然，SimRank算法有很多变种，所以你可能看到其他地方的SimRank算法描述或者迭代的过程和上面的有些不同，但是算法思想基本和上面相同。

SimRank算法有很多改进变种，比较著名的一个改进是SimRank++算法。

4. SimRank++算法原理

SimRank++算法对SimRank算法主要做了两点改进。第一点是考虑了边的权值，第二点是考虑了子集节点相似度的证据。

对于第一点边的权值，上面的SimRank算法，我们对于边的归一化权重，我们是用的比较笼统的关联的边数分之一来度量，并没有考虑不同的边可能有不同的权重度量，而SimRank++算法则在构建转移矩阵W时会考虑不同的边的不同权重值这个因素。

对于第二点的节点相似度的证据。回顾回顾上面的SimRank算法，我们只要认为有边相连，则为相似。却没有考虑到如果共同相连的边越多，则意味着两个节点的相似度会越高。而SimRank++算法利用共同相连的边数作为证据，在每一轮迭代过程中，对SimRank算法计算出来的节点相似度进行修正，即乘以对应的证据值得到当前轮迭代的的最终相似度值。

5. SimRank系列算法的求解

由于SimRank算法涉及矩阵运算，如果用户和物品量非常大，则对应的计算量是非常大的。如果直接用我们第二节讲到了迭代方法去求解，所花的时间会很长。对于这个问题，除了传统的一些SimRank求解优化以外，常用的有两种方法来加快求解速度。

第一种是利用大数据平台并行化，即利用Hadoop的MapReduce或者Spark来将矩阵运算并行化，加速算法的求解。

第二种是利用蒙特卡罗法(Monte Carlo, MC)模拟，将两结点间 SimRank 的相似度表示为两个随机游走者分别从结点 a和 b出发到最后相遇的总时间的期望函数。用这种方法时间复杂度会大大降低，但是由于MC带有一定的随机性，因此求解得到的结果的精度可能不高。

6. SimRank小结

作为基于图论的推荐算法，目前SimRank算法在广告推荐投放上使用很广泛。而图论作为一种非常好的建模工具，在很多算法领域都有广泛的应用，比如我之前讲到了谱聚类算法。同时，如果你理解了SimRank，那么Google的PageRank对你来说就更容易理解了。

个人理解PageRank只能得到某一个节点自己的权重，而SimRank却可以得到两两之间的权重度量，明显SimRank要更加高大上